UNIX forking the universe by running IBM's free online quantum computer

Have you ever been stuck deciding between A or B? React or Svelte? Grad school or industry? Chocolate or vanilla? Wouldn't it be nice if you could split the universe in two, so that at least if you didn't make the right decision, you know there's a version of you in another universe that did?

It might sound crazy, but it takes about 4 seconds to run this circuit, which splits the universe in two and tells you which universe you're in. You can legitimately run it right now.

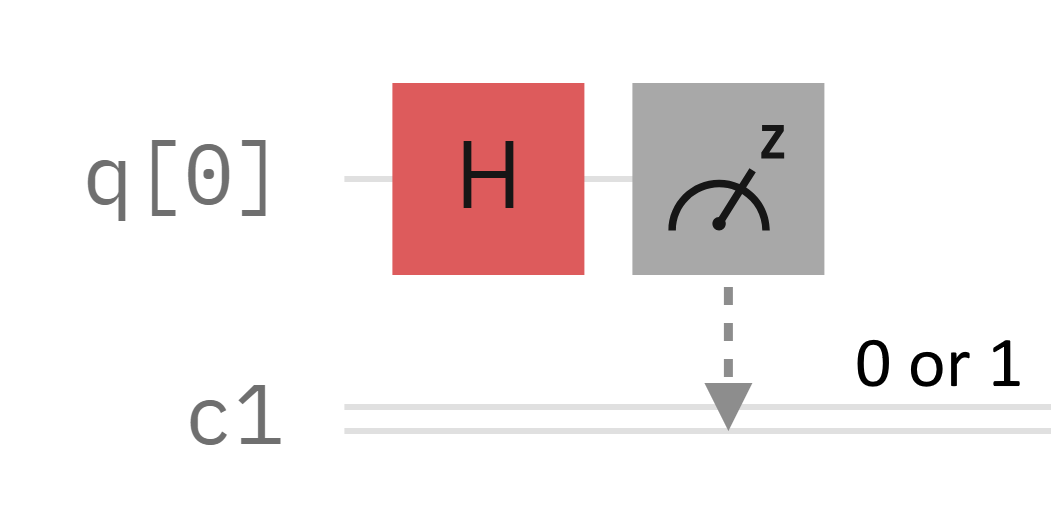
This circuit is basically a unix fork(). It measures a qubit that's in the state $\frac{1}{\sqrt 2}\ket 0 +\frac{1}{\sqrt 2}\ket 1$. I'm keeping math low in this post, but this just means the universe makes a 50/50 decision about whether the qubit is a 0 or a 1, essentially causing the universe to branch in two. In one branch the readout you see is 0, and in the other the readout is 1. You can determine which branch you're in based on the readout, and make your decision based on that info¹.

There are two caveats:

• For this to work, IBM's quantum computer must not have any measurement/decoherence errors. This circuit above is laughably small though, and you can run big circuits today and still get coherent results, so this is usually a valid assumption.

• We're assuming the many-worlds interpretation. But even if you don't believe in many-worlds, I'd argue this is as close as you can get to asking the big man to decide something for you. The outcome provably does not exist until you measure it.² The universe is making a decision for you.

This really works, and it's one of the few useful (maybe) things we can do with quantum computers today. I genuinely think it's a fun & potentially meaningful way to make a decision.